Pitágoras

Se considera a Pitágoras el fundador de una corriente místico-filosófica, el pitagorismo, que alcanzó su esplendor entre los siglos VI y III a.C.
Él descubrió la importancia de los números en la música, y estableció la relación entre la música y la aritmética en los términos matemáticos media armónica y progresión armónica
• Pitágoras descubre que las cuerdas que daban el tono, la cuarta, la quinta y la octava, tenían longitudes proporcionales a 12, 9, 8 y 6. Y puesto que las razones entre los números 12, 9, 8 y 6 son iguales a las que hay entre 1, 3/4, 2/3 y 1/2, que son las más sencillas que se pueden formar con los números de la sagrada Tetractys, 1, 2, 3 y 4, Pitágoras dedujo que ésta es «la fuente y raíz de la Naturaleza eterna» como dicen los Versos Dorados.
• Como en tantos aspectos pitagóricos los números de la Tetractys eran la piedra angular de la armonía musical.
• Mediante una mística extrapolación, la Tetractys sería la fuente del conocimiento de las raíces de la armonía del Cosmos divino, alcanzable a través del número.Si en el número está la clave del tono musical, en él residirá también la clave de toda la naturaleza y en ultima instancia aparecía la matriz de la filosofía pitagórica: «el número es la esencia de todas las cosas»

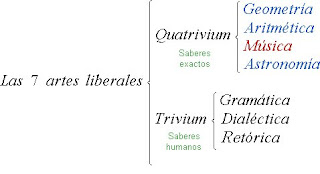
Las siete artes se dividen en “saberes exactos” (Quatrivium o Matemáticas) y “saberes humanos” (Trivium).

Propiedades que comparten Música y Matemáticas

· La primera propiedad, excepcional, que tienen en común la Matemática y la Música es que ambas son lenguajes universales
• La segunda propiedad, es que la teoría física de las ondas juega un papel fundamental en nuestra percepción de la música. Y esta teoría puede ser analizable matemáticamente.
• La tercera propiedad nos la recuerda Bertrand Russell, el matemático puro, como el músico, es creador libre de su mundo de belleza ordenada

Escalas y armonía

Una de las aportaciones más importantes de Pitágoras fue su descubrimiento de que las longitudes de las cuerdas que emiten sonidos armónicos guardan entre sí relaciones numéricas simples: por ejemplo, dada la nota do, para conseguir otro do pero más bajo usaremos una cuerda el doble de larga, es decir, en relación 2:1, y para las notas intermedias en orden ascendente (re, mi, fa...) usaremos cuerdas cuyas longitudes mantengan, respecto de la original, las relaciones 16:9, 8:5, 3:2, 4:3, 6:5, 16:15.

• Pitágoras estaba influenciado por sus conocimientos sobre las medias (aritmética, geométrica y armónica) y el misticismo de los números naturales, especialmente los cuatro primeros (tetrakis).
• Había experimentado que cuerdas con longitudes de razones 1:2 (longitudes 1:2 y 1), 2:3 (media armónica de 1:2 y 1), y 3:4 (media aritmética de 1:2 y 1) producían combinaciones de sonidos agradables y construyó una escala a partir de estas proporciones.
• A estos intervalos los llamó diapasón, diapente y diatesaron. Hoy los llamamos octava, quinta y cuarta porque corresponden a esas notas de la escala pitagórica diatónica (do, re, mi, fa, sol, la, si, do).
Las longitudes de cuerda correspondientes quedan así La proporción entre cada cuerda y la siguiente es de 8:9 (tono), salvo en los casos de fa/mi y do/si, en donde es de 256:243 (hemitono). La pauta entre tonos y hemitonos es 2-h-3-h.
El problema reside en que aplicar dos hemitonos no equivale a aplicar un tono.Además, la distribución de tonos y hemitonos es irregular.

Fórmula de la Escala Diatónica Mayor

T=tono st=semitono
T-T-st-T-T-T-st
Ejemplo para "Do mayor" aplicando la fórmula anterior:
Do (T) Re (T) Mi (st) Fa (T) Sol (T) La (T) Si (st) Do

• La escala usual se obtiene tomando las dos primeras como las mejores combinaciones (octava y quinta) y repitiéndolas sistemáticamente hasta que vuelvan a coincidir. Resulta entonces que 12 quintas equivalen (casi) a 7 octavas.
(3/2)12 / (2:1)7 = 1'0136...
A la diferencia entre estos dos ciclos se le llamó coma pitagórica.

La escala cromática
En 1627 el matemático francés Mersenne (el de los primos 2p-1) formula con precisión la relación entre longitud de cuerda y la frecuencia en su obra Armonía Universal. Esto permitiría la creación de una escala en donde todos los intervalos son iguales (12 semitonos): la escala cromática. Se resolvía así el problema de cambiar de tonalidad (modular) sin reajustar la afinación. La coma pitagórica había desaparecido

• Mientras Bach, Handel, Haydn, Mozart, Beethoven, etc., elevaban la música a alturas de vértigo, dos famosos matemáticos, Euler y d'Alembert, producían teorías de música, continuando la tradición empezada por Descartes (Compendio musical), Galileo (Discurso), Mersenne (Armonía Universal) y Leibniz (en diversas digresiones). Pero la nueva escala cromática necesitaba nuevas teorías de armonía, en las que trabajaron Euler (Nueva teoría musical, en la que trata de ordenar la consonancia, demasiado matemático para los músicos y demasiado musical para los matemáticos) y d'Alembert.
• Música y matemáticas ya se estudiaban por separado